ТЕНЗОРЫ

Таким образом, Эйнштейн усилил картографичность физики, навязав ей воображаемое четырёхмерное пространство, предлагая нам смотреть на мир через четырёхмерную призму его теории. И опять же всё это было продиктовано развитием математики, которая к этому времени прямо-таки потребовала от физиков приложения своих абстрактных математических структур к реальному миру. И Эйнштейн нашёл им применение, сломав сложившееся представление о времени как об абсолютной категории. Этим он приковал к себе внимание научной общественности. И всё это он проделал при помощи особого математического аппарата – тензорного исчисления, применение которого усилило многозначительность его теории.

Тензорное исчисление является обобщением и расширением понятий и действий над векторами.

Известно, что координаты вектора – это строка из нескольких чисел. Перемножив координаты одного вектора на координаты другого вектора, мы получим таблицу. Эту таблицу, в которой первая строка (столбец)  состоит из произведений координат первого вектора на первую координату второго вектора, вторая строка (столбец) из произведений координат первого вектора на вторую координату второго вектора и т.д. называют тензором второго ранга. Обобщая, получаем, что просто число – это тензор нулевого ранга, вектор – это тензор первого порядка, простая двухмерная таблица, получаемая перемножением координат двух векторов – тензор второго порядка, а трёхмерная таблица в виде куба – тензор третьего порядка  и т.д. Для оперирования такими таблицами (тензорами) существуют специальные правила. Это частный случай образования тензора из его общего определения на основе полилинейной формы.   Общее определение тензора через полилинейные формы для физика лишняя нагрузка на мозг и необходимо сказать, что тензор – это просто таблица: ноль мерная как скаляр, одномерная как строка координат вектора, двухмерная как матрица, трёхмерную таблицу ещё можно представить, а вот более мерные уже представить   трудно.   Способ получения тензора валентности два, т.е. квадратной матрицы путём последовательного умножения координат одного вектора , т.е. тензора валентности один, на координаты второго вектора  можно записать следующим образом:

                                     

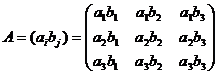
Единичная матрица или, как её называют в тензорном исчислении, симметричный символ Кронекера   получают исходя не из обычного умножения, а из скалярного умножения ортонормированных базисных векторов е_i  и е_j. Их умножают также последовательно, но с учётом того, что скалярное произведение базисного вектора самого на себя равно единице, а скалярное произведение перпендикулярных базисных векторов равно нулю получают:

                           

 

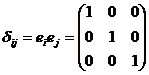
Всё это даёт возможность записать скалярное произведение двух векторов  и  в координатной форме в тензорном виде следующим образом:

                           

Это означает, что сначала последовательным умножением координат первого вектора на координаты второго вектора получают тензор (матрицу) a_ib_j , а затем эту матрицу умножают тем же способом на единичную матрицу (символ Кронекера) и получают известное правило скалярного произведения в координатной форме - скалярное произведение двух векторов равно сумме произведений одноимённых координат этих векторов.  Поэтому умножение квадратной матрицы на символ Кронекера в тензорном исчислении называют свёртыванием тензора a_ib_j. Оно уменьшает валентность тензора на 2. В данном случае из тензора a_ibj  получили скаляр. Свёртываться могут два любых тензора. Для этого элементы одного тензора  последовательно перемножаются на элементы другого тензора, и затем производится сложение по двум любым индексам. Частным случаем такого свёртывания является правило умножения одной матрицы на другую.    Таким образом, правила обращения с тензорами отличаются от правил действия над матрицами.  Тензорное исчисление является обобщением матричного исчисления.

         Существуют и другие способы   образования тензора, например, путём дифференцирования компонент векторной функции по всем переменным. Кроме того все матрицы преобразования одного вектора в другой также являются тензорами. Основная цель тензорной записи - это получить возможность действовать над ними, не обращая внимания на изменение координат    в зависимости от выбора системы отсчёта.

В евклидовом пространстве рассматриваются соотношения   x'₁²+ x'₂²+ x'₃² =  x₁²+ x₂²+ x₃² = const между координатами рассматриваемого события в двух разных системах отсчёта, т.е.   расстояние между двумя точками, которое является инвариантом. Пространство Минковского является псевдоевклидовым, поэтому в нём   рассматривается соотношение x'₀²- x'₁²- x'₂²- x'₃²= x₀²- x₁²- x₂²- x₃² = const. Эйнштейн приспособил тензорное исчисление для изложения ОТО путём введения понятия интервала между двумя событиями в двух разных инерциальных системах отсчёта ct'²- x'₁²- x'₂²- x'₃²= ct²- x₁²- x₂²- x₃² = const, где с – скорость света, t^’ и  t – время в соответствующей системе отсчёта.

Однако, из-за громоздкости оперирования с помощью тензоров таким фундаментальным понятием как время, его теория вошла в массовое сознание лишь своей популистской  спекулятивно-фантастической стороной обещавшая ему возможность вечного существования в другом измерении времени и не привлекла его своим научно-познавательным аспектом. Это можно объяснить тем, что в его рассуждениях нарушался принцип, согласно которого каждая новая теория должна облегчать понимание мира, разрушая нагромождения старых заблуждений, а не усложнять его.

Принятие им противоречивого понятия неравномерного времени,  зависящего от скорости движения тела  не позволило ему создать общую теорию поля,   несмотря на прилагаемые им до конца своей жизни усилия.

                                                                                  См. далее: Резюме по главе 1